一直有一个疑问困扰着我,为什么大部分音乐都是由12个音组成?当然,为了严谨起见,这里所说的音乐并不包括中国传统音乐中的所谓「五声七音十二律」,但其实十二律和现在主流乐音体系中「十二平均律」是相通的。音乐本就无国界,这是一件相当神奇的事情,另外一个例子是全世界各种族的人类听到大三和弦就会感到很愉悦,一旦将大三和弦的中音降低半个音高就会变成小三和弦,这时候听者往往会感到悲伤。
言归正传,作为一个理科生,我还是想从物理学和一点点生理学的角度来研讨一下为什么现代音乐普遍是由12个音谱成。可能有人就要说了钢琴不是有88个键吗?难道不应该是至少有88个音吗?实际上,但从物理学的角度来看,音高就是音的频率高低,那么可用的音就会无穷无尽。但问题是,音的频率只是区分不同音的一个角度,如果从生理学的角度来看,音的频率反而不是很重要,比如,我们将某音乐作品的所有音都按照固定的比率升高之后演奏,就会发现发出的音乐还是和以前一样和谐。所以说,重要的不是音的频率,而是这些频率之间的音程。当我们从C调切换为D调来演奏《小星星》的时候,会发现它还是《小星星》。旋律本身不是一些列音的组合,而是一些列音程的组合。
由此来看,钢琴上的键虽然很多,但是这些键发出的音都是按照固定的比率分组重复,仔细观察就会发现每个分组都包括12个音,其中包括:
- 7个自然音:C-D-E-F-G-A-B
- 5个由自然音变化而来的演化音:C#-D#-F#-G#-A#
这些音的音高关系以及在键盘上的布局如下图所示:
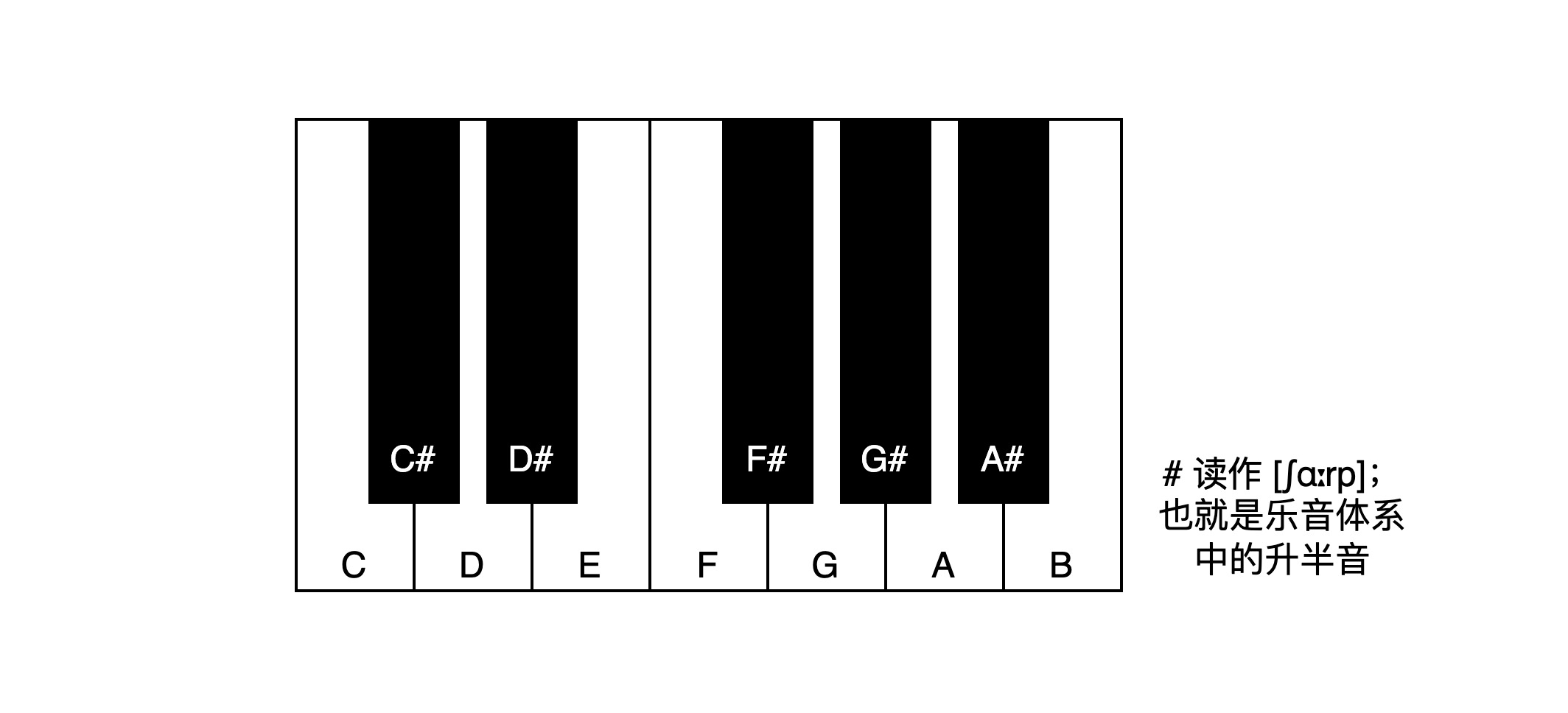
回到上面的问题,为什么会选择这12个音呢?
单从物理学的角度很难回答这个问题,因为音乐本身就是很主观的,之所以选择这12个音是因为经过千万年的演化,大部分人类都认同这12个音以及对应的音程是最和谐悦耳最具音乐性的。说白了就是用这12个音谱成的旋律最适合演奏。
为什么这12个音最适合演奏?
要回答这个问题,就要引出Octave(八度)的概念。钢琴键盘上的所有键是由不同版本的12个音分组组成,我们称之为音组,相邻音组的同名音,我们称之为「八度」。八度是音乐中最和谐最重要的音程,相距八度的音听起来很自洽,它们是相同音的较高或较低表现形式,在乐音体系中称之为Octave Equivalence(八度相等)。从钢琴上看,我们会看到多个A布局在键盘上相邻八度的位置上。而且这种名为八度的音高差异,对应于频率的差异,并非一个固定的赫兹数,而是一个固定的频率比率,该比率为2:1。钢琴中央A音高对应之频率为440Hz,其高八度之A音对应的频率为880Hz;其低八度之A音对应的频率则为220Hz。对于弦乐器,比如吉他,弦长减半,则频率加倍,也就是说弦长一半的音是另一弦的高八度音。
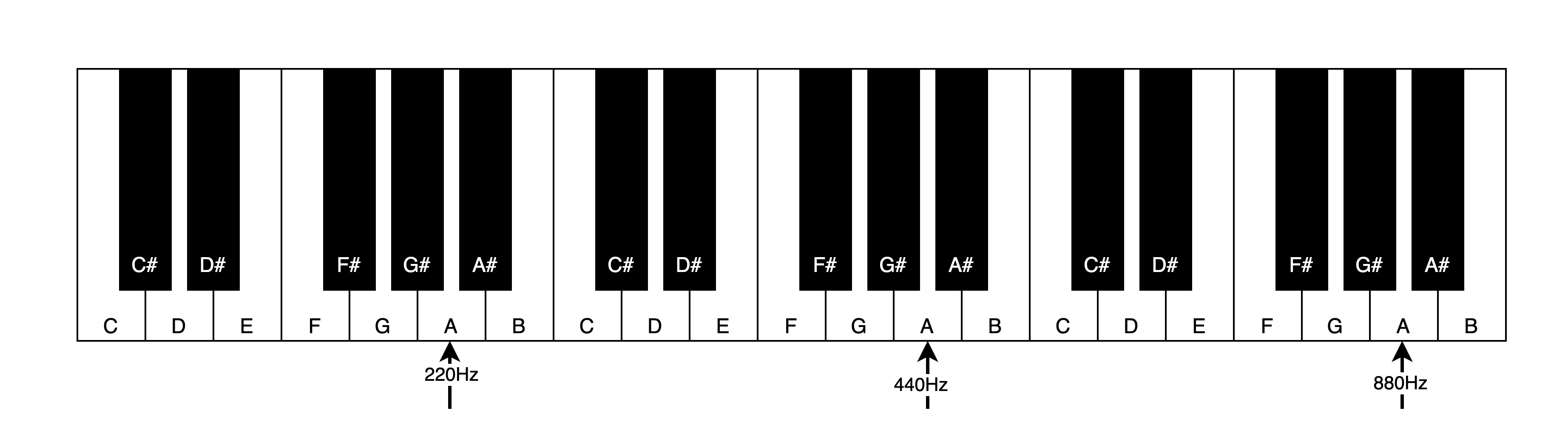
现在世界上主流的音律系统包括西方的十二音律系统(后面会提及)都是首先确定八度,在用各种方式把八度分成不同的音。
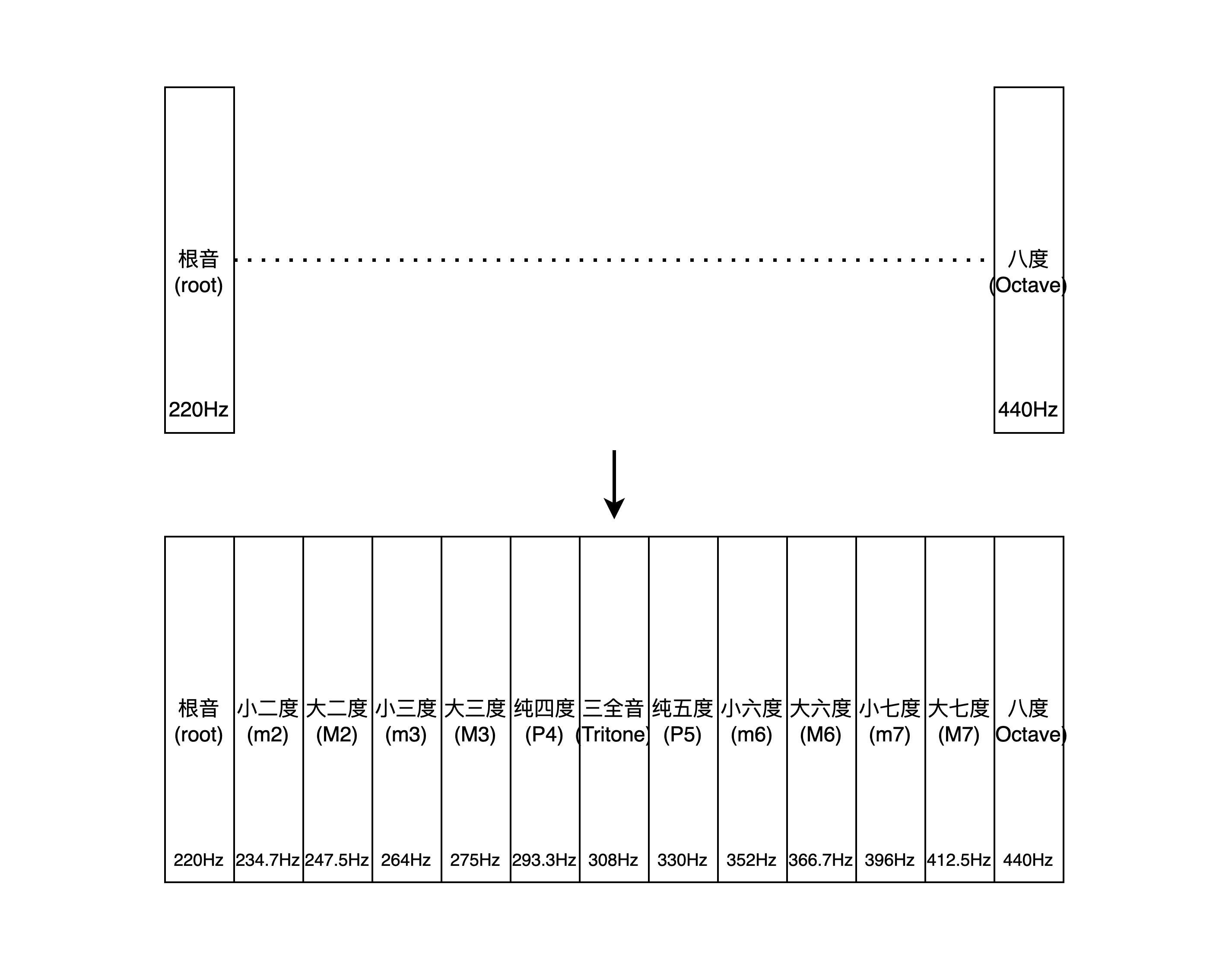
这其中把八度分成12个音的方式可以很方便的演奏下面最重要的几个音程:
其中八度音已经介绍过了,我们快速过一下其他音程,然后再看看它们在键盘上的位置。
除了八度音之外被广泛认为最和谐的两个音程是纯五度与纯四度,其实越是和谐的音程,它们组成音的频率越是具备简单的关系,比如八度音的频率比是2:1,而纯五度与纯四度音的频率比分别是3:2与4:3。
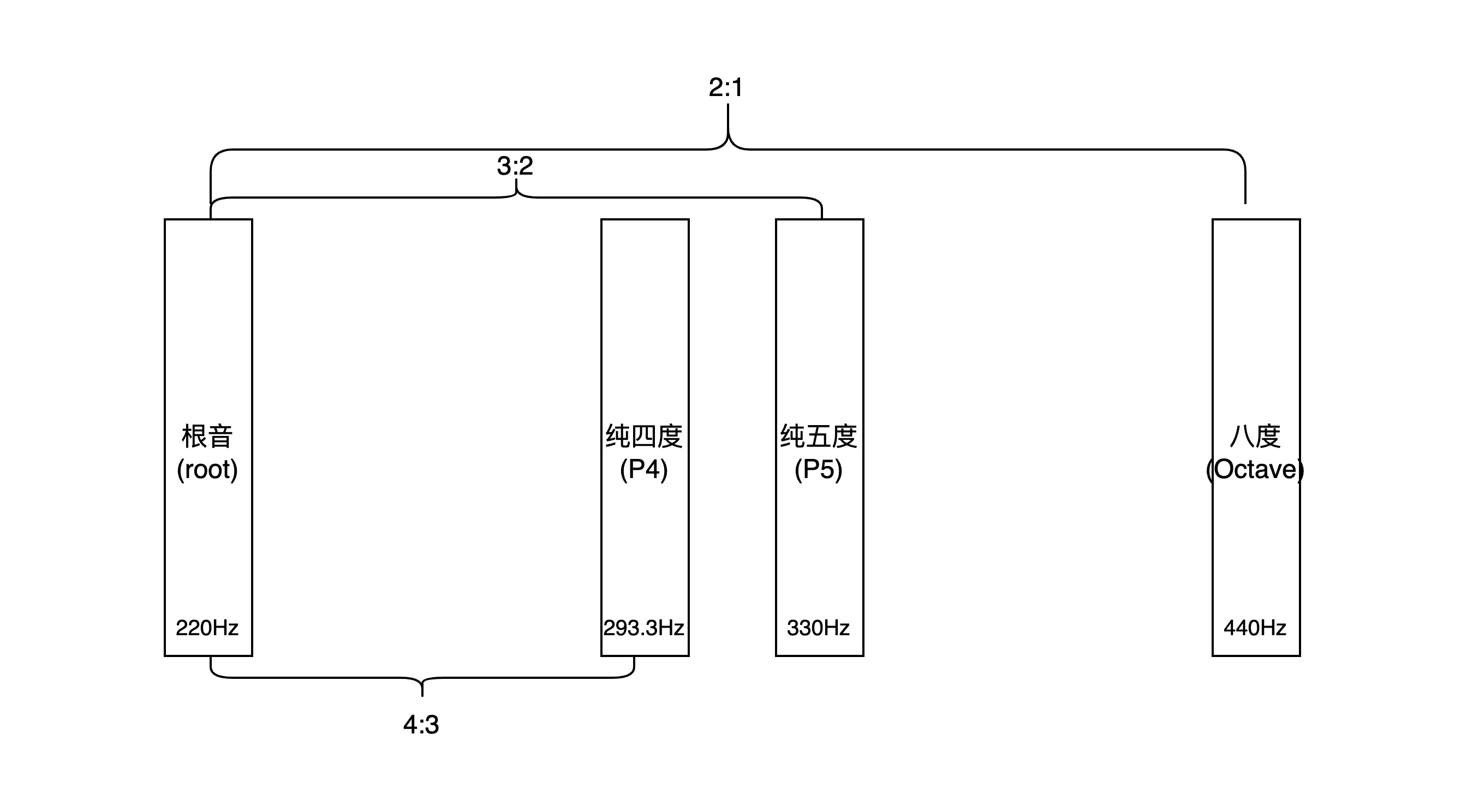
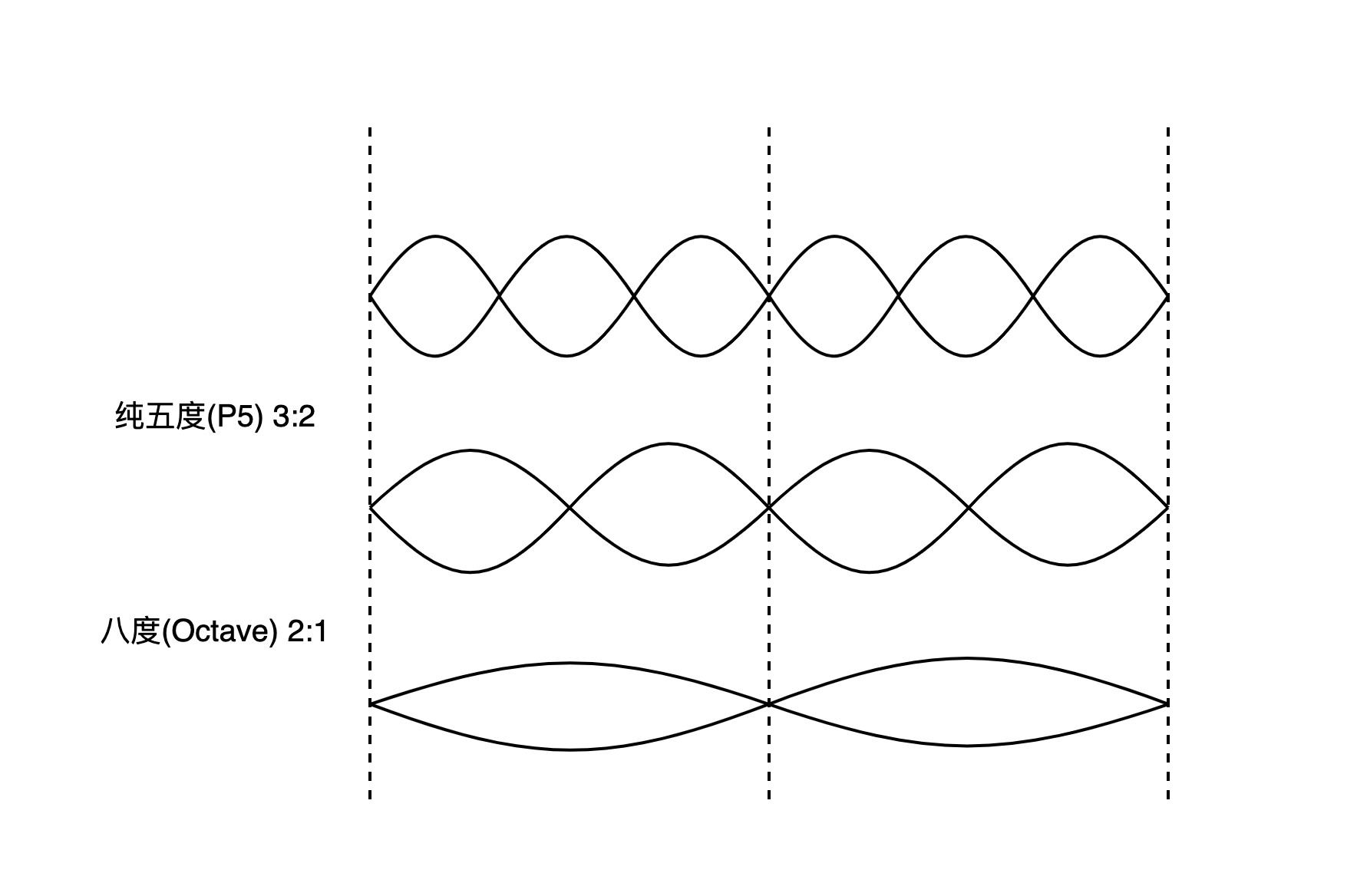
注意这里不要混淆了因果,我们并不是因为音频率比简单而选择它们,而是因为音程越和谐,音之间的频率比越简单。这并不是巧合,从物理学的角度来看,两个音的频率比越简单,这两个音的波长就会完美的排列甚至同步。所以说,音频率的完美同步才是这些音程和谐的根本原因。
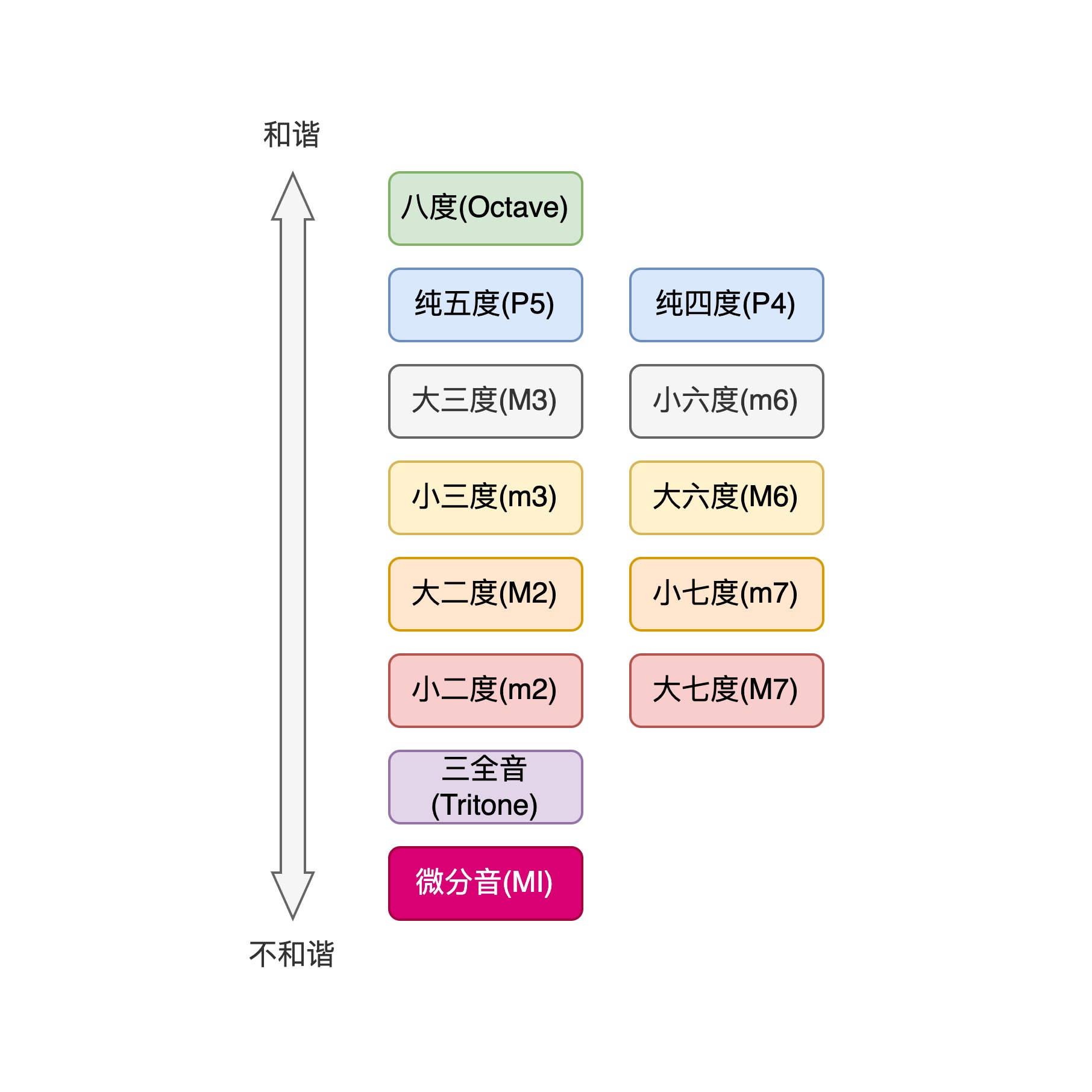
人们对于八度、纯五度与纯四度之外的其他音程和谐程度的排序会略有不同,然而大部分遵循下面这张图,纵坐标代表和谐程度,每个音程的位置越高代表越和谐:

还是列出这些主要和谐音程的频率比,如下表所示,从表中我们也很容易越和谐的音程其组成音的频率比越简单:
| 音程 | 根音的乘阶 | 频率比 |
|---|---|---|
| 八度 | 2 | 2:1 |
| 纯五度 | 1.5 | 3:2 |
| 纯四度 | 1.33 | 4:3 |
| 大三度 | 1.25 | 5:4 |
| 小三度 | 1.2 | 6:5 |
| 大六度 | 1.6 | 8:5 |
| 小六度 | 1.66 | 5:3 |
除了上表所列的和谐音程之外的剩下音程普遍被认为是不和谐的音程,但这并不代表这些音程没有用,虽然说“不和谐”看起来应该尽量避免使用,但是没有“不和谐”音程的音乐往往缺乏戏剧效果或者悬念,所以在某些电影音乐中经常能见到所谓的“不和谐”音程来增加张弛度,最典型的例子就是诺兰电影御用音乐制作大神汉斯-季默的作品。
这基本上就是现代音乐主要用到的12个音。可能有人又要问了,为什么不能在这些音中间再加入一些音,比如,在小三度与大三度之间加入一个“中三度音”,也可以在大七度与八度之间加入一个所谓的“超七音”,这样,就可以这样划分八度之间的音:
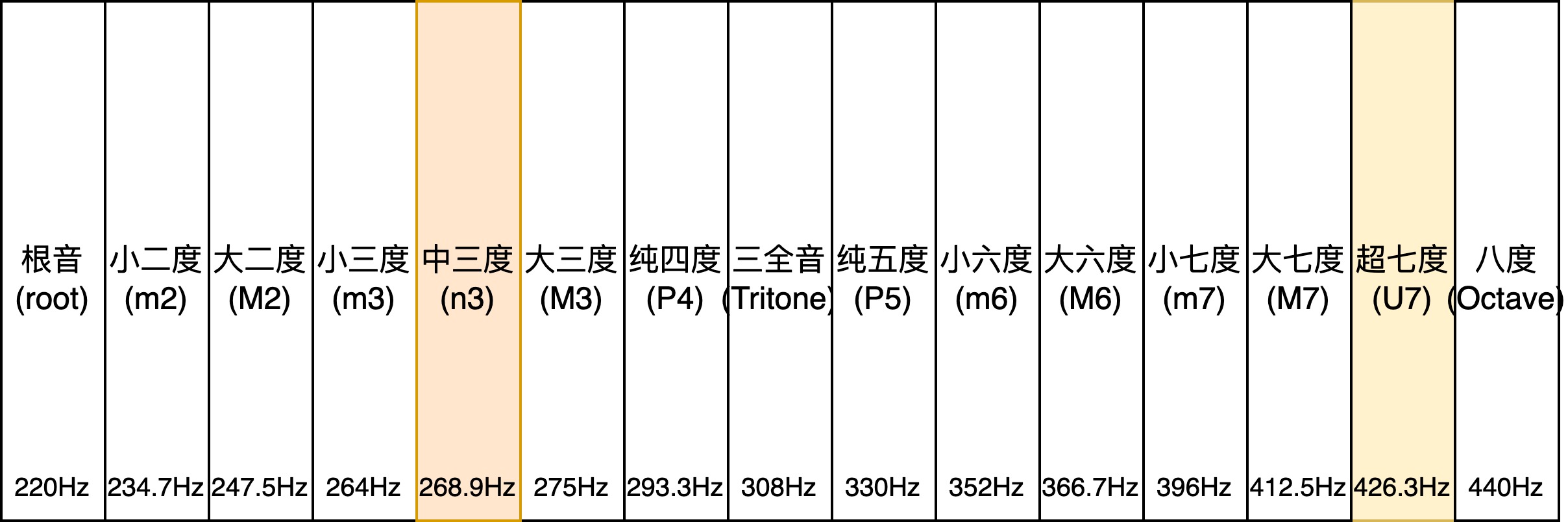
事实上,我们并不能这样加入微分音,因为八度之间的音“几乎”是平均分布的,这方便用乐器演奏不同的调,八度之间的这些标准音几乎是平均排列,如果再加入上面所示的两个微分音,就会打破这种平均的局面。即使要加入更多的音到八度之间,我们也得找到一种既能平均分割八度但又能涵盖上面讲到的各个重要音程(纯五度、纯四度、大三度等)的分割方法。最典型的两种分割方法是:
- 八度19音

- 八度24音

这两种分割方法都既保证了平均布局又保证涵盖各个重要音程,历史上,有些音乐家确实使用这些音律系统制作了乐器并演奏作品,比如四分音钢琴,也叫做24音阶钢琴,每个八度中包含24个键。可想而知,加入更多的微分音会让乐器更加难以演奏,而且这些新加入的微分音符大部分不太实用,也就是说不值得加入乐器。
乐器的设计必须在易用性和演奏更多音之间找到平衡。
几个世纪以来人们经过各种实践得出的结论是,八度12音是这种最优解,它是演奏最和谐和最有用音程的最佳组合方式。有了八度12音,依次增减排列就可以得到钢琴的所有键。
到这里,我们最初的问题似乎得到了解答。
但是,等等…
还有个问题,之前留了一个“坑”,我们提到过上面这种按照简单频率比来划分八度方式得到的12音的布局“几乎”是平均排列但并不是“严格”平均排列,这会不会造成其他的麻烦呢?
要回答此问题?需要介绍新的概念 - 律制
上面介绍的这种律制一般称之为均律,音程按照完美的频率比布局。但是即使是最简单最完美的频率比布局,也会到来其他的问题。因为乐器如果要按照不同的调演奏作品,音就需要尽可能平局排列,所以即使均律12音间隔近似相等,但并不是完美平均排列。

由此带来的问题是,换调演奏同一作品时,根音也跟着发生变化,所以就需要重新调律,但是调律之后就会发生“跑调”的问题。比如A-E之间是完美的3:2关系,所以如果用A大调来演奏音乐听起来会非常悦耳,但是如果在其他调演奏同一音乐,比如Eb大调,听起来就会很不和谐。原因是,虽然A-E的纯五度是完美的3:2关系,但是Eb-Bb的纯五度并不是3:2关系。
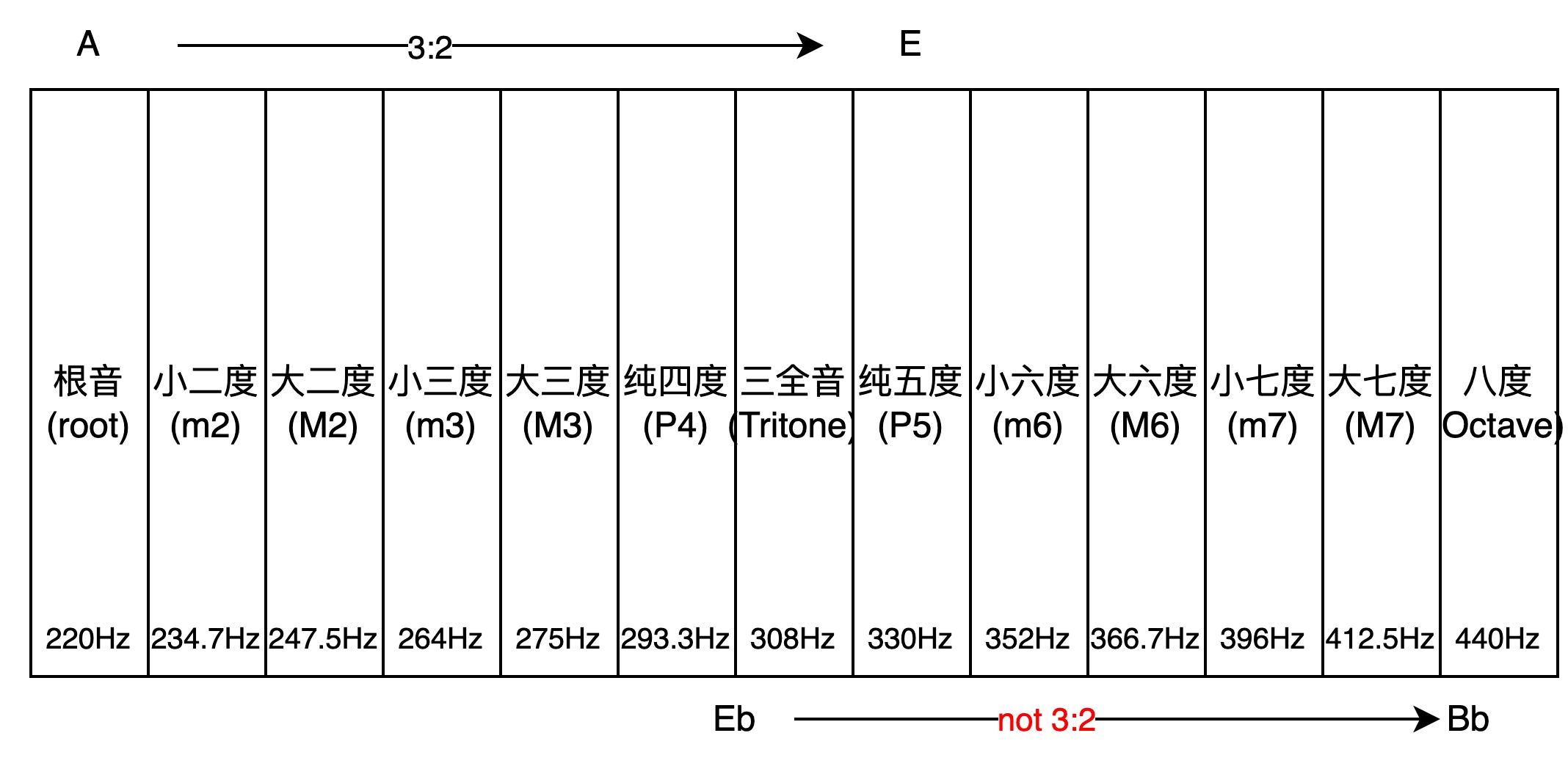
那么,怎么解决这个问题呢?答案是12 Equal Temperament(十二平均律)。
十二平均律保证了相邻音之间的距离严格相等,所以在十二平均律中,A-E是完美的纯五度,Bb-F也是完美的纯五度。

十二平均律除了八度音程还在使用2:1的频率比,不再保证其他各个音程的完美频率比,只不过将八度之间等分为12个音,这种分割方式演奏音乐的能力简单而出色,除了八度之外的其他音程的频率比会和完美比例稍有偏差,但是人耳很难听出这种差别。事实上,几乎我们听到的所有音乐都是使用十二平均律。
到此为止,所有涉及的概念基本都涵盖到了,题目看似简单的问题背后却有如此复杂的原因,既有物理与生理的因素,也有人文历史原因。当然,还是那句话,并不是说音乐只能用这12个音,全世界各种文化中的音乐往往有着不同的音律系统,但是这些音律系统最终的目的还是尽可能兼具实用性与易用性。